Whitepaper (Libro Blanco) del Iota (MIOTA). The Tangle, October 1, 2017. Version 1.3, publicado en www.iota.org.
La Tangle
Serguei Popov∗ , for Jinn Labs April 3, 2016. Version 0.6
1 Introducción y descripción del sistema
El ascenso y el éxito de Bitcoin durante los últimos seis años demostró el valor de la tecnología de la cadena de bloques. Sin embargo, esta tecnología también tiene una serie de inconvenientes, que impiden que sea utilizada como una única plataforma global para cripto monedas. Entre estos inconvenientes, destaca la imposibilidad de realizar micropagos, que han cobrado una importancia cada vez mayor para la industria de Internet de las cosas en rápido desarrollo. Específicamente, en los sistemas actualmente disponibles uno debe pagar una cuota por hacer una transacción; por lo tanto, transferir una cantidad muy pequeña no tiene sentido ya que uno también tendría que pagar la cuota que es muchas veces más grande. Por otro lado, no es fácil deshacerse de las tasas ya que sirven como incentivo para los creadores de los bloques. También debe observarse que las criptodivisas existentes son sistemas heterogéneos con una clara separación de funciones (emisores de transacciones, aprobadores de transacciones). Estos sistemas crean una discriminación inevitable de algunos de sus elementos, lo que a su vez crea conflictos y hace que todos los elementos gasten recursos en la resolución de conflictos. Todo esto justifica una búsqueda de soluciones esencialmente diferentes a la tecnología de la cadena de bloques, en la que se basan el Bitcoin y muchas otras cripto monedas.
En este artículo discutimos un enfoque sin bloques, que actualmente se está implementando en iota[1], diseñado recientemente como una cripto moneda para la industria del Internet-de-Things. Por supuesto, cualquier análisis teórico sería incompleto sin la retroalimentación de una versión operativa de tal sistema; esperamos que pronto dicha retroalimentación esté disponible.
En general, iota funciona de la siguiente manera. En vez de la cadena de bloques global, hay un DAG (= gráfico acíclico dirigido) que llamamos Tangle. Las transacciones emitidas por los nodos constituyen el conjunto de sitios de la Tangle (es decir, el gráfico de Tangle es el libro mayor para almacenar las transacciones). Su conjunto de aristas se obtiene de la siguiente manera: cuando llega una nueva transacción, debe aprobar dos transacciones previas1; estas aprobaciones están representadas por aristas dirigidas, como se muestra en la Figura 1 y otras (en las imágenes, los tiempos siempre van de izquierda a derecha). Si no hay un margen directo entre la transacción A y la transacción B, pero hay un camino directo de longitud al menos dos de A a B, decimos que A aprueba indirectamente B. Existe también la transacción de "génesis", que es aprobada (directa o indirectamente) por todas las demás transacciones, véase la Figura 2. La génesis se describe de la siguiente manera. Al principio había una dirección con un balance que contenía todos los tokens. Entonces la transacción de génesis envió estas fichas a varias otras direcciones de "fundador". Destacamos que todas las fichas fueron creadas en la génesis (no se crearán otras fichas), y no hay minería en el sentido de que "los mineros reciban recompensas monetarias".
Una breve nota sobre la terminología: los sitios son transacciones representadas en el gráfico de la Tangle. La red está compuesta por nodos; es decir, los nodos son entidades que emiten transacciones. Ahora bien, la idea principal es la siguiente: para emitir una transacción, los usuarios deben trabajar para aprobar otras transacciones, contribuyendo así a la seguridad de la red. Se supone que los nodos verifican si las operaciones autorizadas no están en conflicto y no aprueban (directa o indirectamente) las operaciones en conflicto2. A medida que una transacción obtiene más y más aprobaciones (directas o indirectas), se vuelve más aceptada por el sistema; en otras palabras, será más difícil (o incluso prácticamente imposible) hacer que el sistema acepte una transacción de doble gasto. Es importante observar que no imponemos ninguna regla para la elección de las transacciones a aprobar; más bien, argumentamos que si un gran número de otros nodos siguen alguna regla de "referencia" (que parece ser una suposición razonable, especialmente en el contexto de IoT, donde los nodos son chips especializados con firmware preinstalado), entonces para cualquier nodo fijo es mejor seguir una regla del mismo tipo3.
Más específicamente, para emitir una transacción, un nodo hace lo siguiente:
- En primer lugar, elige otras dos operaciones a aprobar (en general, estas dos operaciones pueden coincidir), según algún algoritmo.
- Comprueba si las dos transacciones no son contradictorias y no aprueban las transacciones conflictivas.
Es importante observar que, en general, tenemos una red asincrónica, de manera que los nodos no necesariamente ven el mismo conjunto de transacciones. Cabe señalar también que la Tangle puede contener transacciones contradictorias. Los nodos no tienen que llegar a un consenso sobre qué transacciones válidas4 tienen derecho a estar en el ledger (todas ellas pueden estar allí); pero, en caso de que haya transacciones contradictorias, deben decidir qué transacciones quedarán huérfanas (es decir, no serán aprobadas indirectamente por las transacciones entrantes).
- Para que la transacción sea válida, el nodo debe resolver un rompecabezas criptográfico (que puede ser computacionalmente exigente) similar a los de la minería Bitcoin (por ejemplo, necesita encontrar un nonce de tal manera que el hash de ese nonce junto con algunos datos de las transacciones aprobadas tenga una forma particular, por ejemplo, al menos un número fijo de ceros delante).
La regla principal que los nodos usan para decidir entre dos transacciones conflictivas es la siguiente: un nodo ejecuta el algoritmo de selección de tip5 (cf. Sección 4.1) muchas veces, y ver qué transacción de las dos es más probable que sea (indirectamente) aprobada por el tip seleccionado. Por ejemplo, si, después de 100 ejecuciones del algoritmo de selección de tip, una transacción fue seleccionada 97 veces, decimos que se confirma con un 97% de confianza. Comentemos también la siguiente pregunta (cf.[4]): ¿qué motiva a los nodos a propagar las transacciones? De hecho, en nuestra configuración los nodos no tienen motivación para no propagarse. Cada nodo calcula algunas estadísticas, una de las cuales es cuántas transacciones nuevas se reciben de un vecino. Si un nodo en particular es "demasiado perezoso", será abandonado por sus vecinos. Por lo tanto, incluso si un nodo no emite transacciones (y por lo tanto no tiene ningún incentivo directo para compartir nuevas transacciones que aprueban la suya propia), todavía tiene incentivos para trabajar duro. En las secciones siguientes, después de introducir algunas anotaciones en la Sección 2, discutimos los algoritmos para elegir las dos transacciones a aprobar, las reglas para medir la aprobación de la transacción global (Sección 3 y especialmente la Sección 3.1), y los posibles escenarios de ataque (Sección 4). Además, en el improbable caso de que el lector se asuste por las fórmulas, puede saltar directamente a la parte de "conclusiones" al final de la sección correspondiente.
Cabe señalar que las ideas sobre el uso de los DAGs en el contexto cripto-divisa estuvieron presentes durante algún tiempo, por ejemplo [3,5,6,7,10]. Específicamente, el trabajo [6] introduce el denominado protocolo GHOST, que propone una modificación del protocolo Bitcoin haciendo del libro mayor un árbol en lugar de la cadena de bloques; se demuestra que dicha modificación permite reducir los tiempos de confirmación y mejorar la seguridad global de la red. En el documento [7] los autores consideran un modelo criptográfico basado en DAG; a diferencia de nuestro modelo, los sitios del DAG son bloques (no transacciones individuales), los mineros compiten por los honorarios de las transacciones, y (como en Bitcoin) se pueden crear nuevos tokens. También, observe que en el trabajo [5] se propuso una solución algo similar a la nuestra, aunque no se discute ninguna estrategia particular de aprobación de tips. Mencionamos también otro enfoque [2,8] que pretende hacer posibles los micropagos de Bitcoin mediante el establecimiento de canales de pago peer-to-peer.
2 Pesos y mas
Aquí, definimos el peso (propio) de una transacción y los conceptos relacionados. El peso de una transacción es proporcional a la cantidad de trabajo que el nodo emisor invirtió en ella; en la práctica, el peso sólo puede asumir los valores 3n, donde n es un número entero positivo y pertenece a algún intervalo no vacío de valores aceptables6. Una de las nociones que necesitamos es el peso acumulativo de una transacción: se define como el propio peso de esta transacción más la suma de los pesos propios de todas las transacciones que aprueban nuestra transacción directa o indirectamente. Este algoritmo de cálculo de ponderaciones acumulativas se ilustra en la figura 1. Los recuadros representan las transacciones; los números pequeños en la esquina SE representan el propio peso de las transacciones, mientras que los números en negrita (mayores) son los pesos acumulados. Por ejemplo, la operación F está autorizada, directa o indirectamente, por las operaciones A, B, C, E. El peso acumulado de F es 9 = 3 + 1 + 3 + 3 + 1 + 1 + 1 + 1, la suma del peso de F y los pesos de A, B, C, E. En la imagen superior, las únicas operaciones no autorizadas (las "tips") son A y C. Cuando la nueva operación X llega y aprueba A y C, se convierte en la única tip, el peso acumulado de todas las otras transacciones incrementa en 3 (que es el peso de X).
Figura 2: Sobre el cálculo de los puntajes (circulo)
- height, como la longitud de la trayectoria más larga orientada a la génesis;
- depth, como la longitud de la trayectoria inversa más larga a alguna tip.
Por ejemplo, en la Figura 2, G tiene altura 1 y profundidad 3 (debido a la trayectoria inversa F, B, A), mientras que D tiene altura 2 y profundidad 2. Además, introduzcamos la noción de la partitura. Por definición, la puntuación de una transacción es la suma de los pesos propios de todas las transacciones aprobadas por esta transacción más el propio peso de la transacción Vea la figura 2. Nuevamente, los únicos tips son A y C. La transacción A aprueba (directa o indirectamente) las transacciones B, D, F, G, por lo que la puntuación de A es 1 + 3 + 1 + 3 + 3 + 1 = 9. Análogamente, la puntuación de C es 1 + 1 + 1 + 1 + 3 + 3 + 1 = 7. También, observemos que, entre las métricas anteriores, el peso acumulativo es lo más importante para nosotros (aunque las alturas, profundidades y puntuaciones entrarán brevemente en algunas discusiones también).
3 Estabilidad del sistema y cutsets
Supongamos que L(t) es el número total de tips (i.e, transacciones todavía no aprobadas) en el sistema a tiempo t. Uno, por supuesto, espera que el proceso estocástico L (t) se mantenga estable7 (más precisamente, positivamente recurrente; véanse las secciones 4.4 y 6.5 de[9] para las definiciones formales; en particular, la recurrencia positiva implica que el límite de P[L (t) = k) a t → ∞ debería y ser positivo para todos los k ≥ 1). Intuitivamente, esperamos que L (t) fluctúe alrededor de un valor constante, y no escape al infinito (dejando así muchas transacciones no aprobadas). Para analizar las propiedades de estabilidad de L (t), necesitamos algunos supuestos. Supongamos que 𝜆 es el ritmo del flujo de entrada (Poisson) de transacciones; por simplicidad, asumamos por ahora que se mantiene constante. Supongamos que todos los dispositivos tienen aproximadamente la misma potencia computacional, y que h (L, N) sea el tiempo promedio que un dispositivo necesita para hacer los cálculos necesarios para emitir una transacción en la situación cuando hay L tips y el número total de transacciones es N. Primero, consideramos la estrategia cuando, para emitir una transacción, un nodo sólo elige dos tips al azar y las aprueba. En este caso, uno puede asumir que los flujos de aprobaciones de Poisson a las diferentes tips son independientes, y tienen tasa 𝜆/L (esto sigue por ejemplo de la Proposición 5.2 de[9]). Por lo tanto,
ℙ[nadie aprueba un determinado tip durante el tiempo h (L,N)]=exp(−𝜆ℎ(𝐿,𝑁)/𝐿) (1).
Esto significa que el incremento esperado del número total de tips en el momento en que nuestro dispositivo emite una transacción es igual a
1 − 2 𝑒𝑥𝑝 (−𝜆ℎ(𝐿,𝑁)/𝐿) (2)
(en la fórmula anterior, "1" corresponde a la nueva tip creada por la transacción, y el segundo término es el número esperado de tips "borrados"). Ahora, L(t) es de hecho un paseo aleatorio continuo en N = {1,2,3,. . .} con transiciones más cercanas a los vecinos. De hecho, si las dos transacciones elegidas ya fueron aprobadas por otros, entonces el proceso salta una unidad a la izquierda, si ambas transacciones elegidas no fueron aprobadas, entonces el proceso salta una unidad a la derecha, y en el último caso posible permanece en el mismo lugar.
Ahora, para entender el comportamiento típico del proceso, observe que la deriva en (2) es positiva para L pequeña y negativa (al menos en el caso de que h(L,N) = o (L) como L → ∞; o simplemente asumiendo que la contribución principal al tiempo de computación/propagación no viene del manejo de las tips) para L. El valor "típico" de L sería donde (2) se desvanece, es decir, L0 tal que.
L0 ≈ λh(L0,N)/ln(2)≈ 1.44 · λh(L0,N). (3)
Además, observe que (al menos en el caso de que los nodos intenten aprobar las tips) en cualquier momento fijo t el conjunto de transacciones que eran tips en algún momento s pertenece [t, t+h (L0, N)] típicamente constituye un cutset, en el sentido de que cualquier ruta desde una transacción emitida en el momento t 0 > t hasta la génesis debe pasar a través de este conjunto. Es importante que el tamaño de los cutsets sea pequeño por lo menos de vez en cuando; entonces se puede utilizar los pequeños cutsets como puntos de control, para posibles podas de DAG y otras tareas. Ahora bien, la estrategia anterior "puramente aleatoria" no es muy buena en la práctica, porque no fomenta la aprobación de tips: un usuario "perezoso" podría aprobar siempre un par fijo de transacciones muy antiguas (y por lo tanto no contribuir a la aprobación de transacciones más recientes) sin ser castigado por tal comportamiento8. Para desalentar el comportamiento de este tipo, hay que adoptar una estrategia que se inclina hacia las tips con mayor puntuación. Un ejemplo de tal estrategia puede ser el siguiente. Fijar un parámetro α ∈ (0,1); a continuación, seleccione las dos transacciones que desea aprobar entre las dos primeras 𝛼L (con respecto a su puntaje). Las mismas consideraciones anteriores implican que el tamaño típico del conjunto de tips será.
En cuanto al momento previsto para la primera aprobación de una transacción, la situación es un poco más complicada. Antes de comenzar la discusión sobre el tiempo esperado para que una transacción sea aprobada por primera vez, observe que podemos distinguir esencialmente dos regímenes (ver Figura 3).
- Carga baja: el número típico de tips es pequeño, e incluso con frecuencia se convierte en 1. Esto puede suceder cuando el flujo de transacciones es lo suficientemente pequeño, de modo que no es probable que varias transacciones diferentes aprueben el mismo tip; también, si la latencia de la red es muy baja y los dispositivos calculan rápidamente, entonces, incluso en la situación en que el flujo de transacciones es razonablemente grande, también es poco probable que aparezcan muchos tips. Además, tenemos que asumir que no hay atacantes que intenten inflar artificialmente el número de tips.
- Carga alta: el número típico de tips es grande. Esto puede suceder cuando el flujo de transacciones es suficientemente grande, y los retrasos computacionales junto con la latencia de la red hacen probable que varias transacciones diferentes aprueben el mismo tip.
Figura 3: La Tangle y sus tip típicas se ponen (sombreada) en regímenes de carga baja y alta. Observe que, en este último caso, es posible que algunas transacciones tengan que esperar mucho hasta que se aprueben por primera vez.
Por supuesto, esta división es bastante informal y no hay una frontera clara entre los dos regímenes; sin embargo, consideramos que puede ser instructivo considerar estas dos situaciones esencialmente diferentes.
En el régimen de baja carga, la situación es relativamente simple: la primera aprobación se produce en el tiempo medio de pedido 𝜆-1, ya que la primera (o una de las primeras) transacciones entrantes aprobará nuestra transacción.
Consideremos ahora el régimen de alta carga. En primer lugar, si la transacción no ha llegado al top αL, entonces este tiempo de espera puede ser bastante grande, de orden exp(c𝐿0 𝛼) (ya que hay una desviación hacia 𝐿0 𝛼 para valores menores de L y el tamaño de tips tiene que ser mucho menor que 𝐿0 𝛼 para que esa transacción sea considerada para aprobación). Por lo tanto, una buena estrategia para el propietario de tal transacción sería emitir una transacción vacía adicional haciendo referencia a la primera, y esperar que esta nueva transacción entre en la parte superior de la lista. También, de manera similar a lo anterior, si la transacción es una de las primeras αL, entonces con probabilidad constante tendrá que esperar alrededor de L0/ 𝜆 unidades de tiempo para ser aprobadas por primera vez (observe que α𝐿0 𝛼 = L0). Sin embargo, si eso no ocurrió, entonces la transacción puede caer por debajo de top αL, y entonces una buena estrategia será promoverla con una transacción vacía adicional. Otra estrategia fácil sería elegir, por ejemplo, cinco tips al azar (entre todos ellos), y aprobar los dos primeros entre estos cinco. Una vez más, si su transacción no fue aprobada durante un tiempo Θ(L0/𝜆) = Θ (h(L0, N)), es una buena idea promoverla con una transacción vacía adicional. También advertimos que la estrategia de aprobación puede ser modificada, por ejemplo, para prevenir el spamming. Por ejemplo, los nodos pueden preferir tips con mayor peso propio, haciendo más difícil que el spammer tenga sus transacciones aprobadas. Ahora, resulta que las estrategias de aprobación basadas en alturas y puntuaciones pueden ser vulnerables a un tipo específico de ataques, véase la Sección 4.1. Discutiremos estrategias más elaboradas9 para defenderse contra tales ataques en esa sección. Sin embargo, todavía vale la pena considerar la estrategia de selección de la tip más simple ("aprobar dos tips aleatorias"), ya que es la más fácil de analizar, y por lo tanto puede dar una cierta perspicacia sobre el comportamiento cualitativo y cuantitativo del sistema.
Conclusiones:
1. Distinguimos entre dos regímenes, carga baja y carga alta, como se muestra en la Figura 3.
2. En el régimen de baja carga, por lo general no hay muchas tips (digamos, una o dos), y una tip es aprobada por primera vez en Θ (𝜆−1), donde 𝜆 es la tasa del flujo de entrada de transacciones.
3. En el régimen de alta carga, el número típico de tips depende de la estrategia de aprobación (es decir, cómo la nueva transacción elige las otras dos transacciones para su aprobación).
4. Para la estrategia de "aprobar dos tips aleatorios", el número típico de tips viene dado por (3). Se puede demostrar que esta estrategia es óptima con respecto al número típico de tips; sin embargo, no es práctico adoptarla porque no fomenta la aprobación de tips.
5. Para la estrategia "aprobar dos tips aleatorias entre los top 𝛼L (t)" (que no tiene la desventaja anterior), el número típico de tips es dado por (4).
6. Sin embargo, se necesitan estrategias más elaboradas; en la sección 4.1 se describirá una familia de dichas estrategias.
7. En el régimen de alta carga, el tiempo típico hasta que se aprueba una tip es Θ(h), donde h es el tiempo medio de cálculo/propagación para un nodo. Sin embargo, si la primera aprobación no se produjo en el intervalo de tiempo anterior, es una buena idea (para el emisor/receptor) promover esa transacción con una transacción vacía adicional.
3.1 ¿Qué tan rápido crece el peso acumulado?
En el régimen de baja carga, después de que nuestra transacción sea aprobada varias veces, su peso acumulativo crecerá con speed 𝜆w, donde w es el peso promedio de una transacción genérica, ya que esencialmente todas las nuevas transacciones indirectamente harán referencia a nuestra transacción.
En cuanto al régimen de alta carga, como se ha observado anteriormente en esta sección, si una transacción es lo suficientemente antigua y con un gran peso acumulativo, entonces el peso acumulado crece con la velocidad 𝜆w por las mismas razones. Además, vimos que al principio la transacción puede tener que esperar algún tiempo para ser aprobada, y está claro que su peso acumulativo se comporta de manera aleatoria en ese momento. Para ver, qué tan rápido crece el peso acumulativo después de que la transacción obtiene varias aprobaciones, deje que el uso denote (por simplicidad, comenzamos a contar el tiempo en el momento en que nuestra transacción ha sido creada) por H (t) el peso acumulativo esperado en el momento t, y por K (t) el número esperado de tips que aprueban nuestra transacción en el momento t (o simplemente "nuestros tips"). Abreviemos también h := h (L0, N). También, hacemos una suposición simplificadora que el número total de tips permanece aproximadamente constante (equivalente a L0) en el tiempo. Trabajamos con la estrategia de "aprobar dos tips aleatorios" aquí; se espera que el resultado sea aproximadamente el mismo para la estrategia de "aprobar dos tips aleatorios en top 𝛼L (t)".
Observe que una transacción que llega al sistema en el momento t normalmente elige las dos transacciones a aprobar basándose en el estado del sistema en el momento t - h. No es difícil obtener que la probabilidad de que apruebe al menos "nuestra" tip es
Análogamente e.g. al Ejemplo 6.4 de [9], podemos escribir.
y así deducir la siguiente ecuación diferencial
Para poder utilizar (5), primero necesitamos calcular K (t). No está claro de inmediato cómo hacerlo, ya que una tip en el momento t-h puede no ser una tip en el momento t, y, en el caso de que la nueva transacción apruebe tal tip, el número total de tips que aprueben la transacción original aumentará en un punto. Ahora, la observación crucial es que la probabilidad de que una tip en el tiempo t - h permanezca como una tip en el tiempo t es aproximadamente 1/2, recordar (1) y (3). Así que, a tiempo t esencialmente la mitad de K (t-h) "anterior" nuestras tips siguen siendo tips, mientras que la otra mitad ya será aprobada al menos una vez. Denotemos por A el conjunto de esos (aproximadamente) K (t - h)/2 tips en el tiempo t - h que quedaron tips a tiempo t, y el conjunto de otros tips K (t - h)/2 tips (que ya fueron aprobados) serán denotados por B. Dejemos que p1 sea la probabilidad de que la transacción recién llegada apruebe por lo menos 1 transacción de B y no apruebe ninguna transacción de A. También, dejemos que p2 sea la probabilidad de que ambas transacciones aprobadas pertenezcan a A. Claramente, p1 y p2 son, respectivamente, las probabilidades de que el número actual de "nuestras" tips aumente o disminuya en 1 a la llegada de la nueva transacción. Tenemos
(para obtener la primera expresión, observe que p1 es igual a la probabilidad de que ambas tips aprobadas pertenezcan a B más dos veces la probabilidad de que la primera tip pertenezca a B y la segunda tip no pertenezca a A U B). Análogamente a (5), la ecuación diferencial para K (t) entonces se escribe:
Es difícil de resolver (6) exactamente, por lo que simplificamos aún más los supuestos. En primer lugar, observamos que, después del tiempo en que K(t) alcanza el nivel εL0 para un ajustado ε > 0, crecerá muy rápidamente casi hasta L0. Ahora, cuando K(t) es pequeño con respecto a L0, podemos dejar caer el último factor en el lado derecho de (6). Además, sustituyendo K (t - h) por K (t) - h 𝑑𝐾 (𝑡)/𝑑𝑡, obtenemos una versión simplificada de (6) (recordemos que 𝜆ℎ/𝐿0 = ln 2):
con la condición límite K (0) = 1. Esta ecuación diferencial resuelve a
Así que, tomando los logaritmos en (8), encontramos que el tiempo cuando K (t) alcanza εL0 es aproximadamente
Volviendo a (5) (y, como antes, dejando caer el último término en el lado derecho) obtenemos que durante el "período de adaptación" (es decir, t ≤ 𝑡0 con 𝑡0 como en (9)), sostiene que
Y también
Recordemos al lector que, como se ha comentado anteriormente, después del período de adaptación el peso acumulativo H (t) crece esencialmente linealmente con la velocidad λw. Subrayamos que el "crecimiento exponencial" (como en (10) no significa que el peso acumulativo crezca "muy rápidamente" durante el período de adaptación; más bien, el comportamiento es como se muestra en la Figura 4.
Además, comentamos que los cálculos de esta sección pueden ser fácilmente adaptados a la situación cuando un nodo hace referencia a s > 1 transacciones en promedio. Para ello, basta con sustituir 2 por s en (2) (pero no en (5)!), y ln(2) por ln(s) en (3)-(4) y en (7)-(10).
Conclusiones:
1. En el régimen de carga baja, después de que nuestra transacción sea aprobada varias veces, su peso acumulativo crecerá con speed λw, donde w es el peso medio de una transacción genérica.
2. En el régimen de alta carga, nuevamente, después de que nuestra transacción es aprobada varias veces, primero su peso acumulativo H (t) crece con mayor velocidad durante el llamado período de adaptación de acuerdo a la fórmula (10), y luego de finalizado el período de adaptación, crece con la velocidad λw, ver Figura 4. De hecho, para cualquier estrategia razonable, el peso acumulado crecerá con esta velocidad después del final del período de adaptación, porque esencialmente todas las transacciones que se reciban en breve aprobarán indirectamente nuestra transacción.
Figura 4: Sobre el crecimiento del peso acumulado
3. Uno puede pensar que el período de adaptación es el tiempo hasta que la mayoría de los tips actuales (indirectamente) aprueban nuestra transacción. La duración típica del período de adaptación viene dada por (9).
4 Posibles escenarios de ataque
Describamos un escenario de ataque:
1. el atacante paga al comerciante, y recibe las mercancías después de que el comerciante considera que la transacción ya tiene un peso acumulativo suficientemente grande;
2. el atacante emite una transacción de doble gasto;
3. el atacante emite un montón de pequeñas transacciones (muy agresivamente, con toda su potencia de computación) que no aprueban la original directa o indirectamente, sino que aprueban la transacción de doble gasto;
4. Observa que el atacante puede tener muchas identidades de Sybil, y que no está obligado a aprobar tips;
Figura 5: El “large weight attack”
5. Alternativamente al punto 3, el atacante puede usar toda su potencia de computación para emitir una transacción "grande" de doble gasto (es decir, con un peso propio muy grande) que aprueba un par de transacciones previas a la legítima (la que se usaba para pagar al comerciante);
6. espera que su "subDAG" supere al principal, de modo que el DAG siga creciendo a partir de la operación de doble gasto, y la rama legítima sea desechada (ver Figura 5).
De hecho, veremos a continuación que la estrategia de una gran transacción de doble gasto aumenta las posibilidades del atacante. Aún más, en la situación "ideal" de este modelo matemático, este ataque siempre tiene éxito.
De hecho, W (n) es el tiempo necesario para obtener un nonce que da peso al menos 3n a la transacción de doble gasto. Se puede suponer que W (n) es una variable aleatoria distribuida exponencialmente con el parámetro μ3-n (es decir, con la expectativa μ-1 3n), donde μ mide la potencia de cálculo del atacante.
Supongamos que el comerciante acepta la transacción legítima cuando su peso acumulativo se convierte en por lo menos w0 (y esto sucede 𝑡0 unidades de tiempo después de la transacción original), y entonces es razonable esperar que el peso acumulativo crezca con la velocidad lineal λw donde λ es la tasa de llegada total de transacciones al sistema (emitido por usuarios honestos) y w es el peso medio de una transacción genérica. Denote w1 = λw𝑡0, el peso total típico de la rama legítima en ese momento.
Siendo [x] el número entero más pequeño mayor o igual a x, define n0 = ln w1 en w1 en 3, de modo que 3n0 ≥ w1 (de hecho, 3n0 ≈ w1 si w1 es grande). Si durante el intervalo de tiempo de la longitud 𝑡0 el atacante logró obtener un nonce que da un peso de al menos 3n0, entonces el ataque tiene éxito. La probabilidad de este evento es
(al menos en el caso de que 𝑡0μ/𝑤1 sea pequeño, lo cual es una suposición razonable). Entonces, si este ataque "inmediato" no tuvo éxito, el atacante puede seguir buscando el nonce que da peso 3n para n > n0, y esperar que en el momento en que lo encuentre, el peso total de la rama legítima sea menor que 3n. Ahora, la probabilidad de esto es
Es decir, aunque μ/𝜆𝑤 debería ser típicamente pequeño, en cada "nivel" n el ataque tiene éxito con una probabilidad constante. Por lo tanto, finalmente tendrá éxito a. s.. De hecho, el tiempo típico hasta que tiene éxito es de aproximadamente 3𝜆𝑤7μ. Aunque esta cantidad puede ser muy grande, aún así la probabilidad de que incluso el "primero" ataque (i.e., durante el tiempo t0) tenga éxito, no es muy pequeña. Llegamos así a la siguiente conclusión: necesitamos contramedidas. Por ejemplo, limitar el propio peso desde arriba, o incluso ponerlo en constante (como se menciona en la Sección 3, esta última puede no ser la mejor solución, ya que no ofrece suficiente protección contra el spam).
Ahora, vamos a discutir la situación cuando el peso máximo es limitado, por ejemplo, por m, y estimar la probabilidad de que el ataque tenga éxito.
En vista de la discusión anterior (y también usando alguna intuición general de la Teoría de las Grandes Desviaciones [11]), si el atacante quiere alcanzar la cadena principal, sólo debe producir transacciones con el peso máximo permitido. Supongamos que una transacción determinada ha ganado un peso acumulativo w0 en t0 unidades de tiempo después del momento en que se emitió. Supongamos también que el período de adaptación para esa transacción ha terminado, y por lo tanto su peso acumulativo aumenta linealmente con velocidad λw. Ahora, el atacante quiere gastar doblemente en esta transacción; para ello, en el momento10 en que se emitió la primera transacción, prepara secretamente la transacción de gasto doble, y comienza a generar otras transacciones con peso m que aprueban la de gasto doble. Si en algún momento (después de que el comerciante decide aceptar la transacción legítima) la subTangle del atacante sobrepasa a la legítima subTangle, entonces el ataque de doble gasto sería exitoso. Si eso no sucede, entonces la transacción de doble gasto no será aprobada por otros (ya que la transacción legítima adquirirá más peso acumulativo y esencialmente todas las nuevas tips lo aprobarían indirectamente), por lo que quedará huérfana.
Como antes, supongamos que μ representa la potencia de cálculo del atacante. Deja G1, G2, G3,. . . Denota i. i. d. d. Variables aleatorias exponenciales con parámetro μ/m (es decir, con valor esperado m/μ) y denotar también Vk = μ/𝑚 Gk, k ≥ 1. Claramente, V1, V2, V3,. . . son identificadores internos. Variables aleatorias exponenciales con parámetro 1.
Supongamos que en el momento t0 el comerciante decidió aceptar la transacción (recuerde que en ese momento tiene un peso acumulativo w0). Estimemos la probabilidad de que el atacante realice con éxito un doble gasto. Deje que M(θ) = (1−𝜃)−1 sea la función generadora de momentos (ver Sección 7.7 de[12]) de la Distribución exponencial con el parámetro 1. Se sabe (además del libro general[11], véase también la Proposición 5.2 en la Sección 8.5 de[12], aunque no explica por qué la desigualdad debería ser, de hecho, una igualdad aproximada) que para α ∈ (0,1) sostiene que
donde ϕ(α) = − ln α + α − 1 es la transformada de Legendre de ln M (-θ). Obsérvese que, como un hecho general, sostiene que ϕ(α) > 0 for α ∈ (0, 1) (recuerde que la expectativa de una variable aleatoria Exp (1) equivale a 1).
Supongamos también que μ𝑡0/𝑤0 < 1 (de lo contrario, la probabilidad de que la subTangle del atacante supere eventualmente al legítimo sería cercana a 1). Ahora, para sobreponderar w0 a tiempo t0, el atacante necesita ser capaz de emitir por lo menos w0/m (para simplificar, ignoramos las integraciones) transacciones con un peso máximo m durante el tiempo t0. Por lo tanto, utilizando (11), obtenemos que la probabilidad de que la transacción de gasto doble tenga más peso acumulativo en el momento t0 es aproximadamente.
Es decir, para que la probabilidad anterior sea pequeña, normalmente necesitamos que w0 m sea grande y ϕ (μ𝑡0/𝑤0) no muy pequeña.
Tenga en cuenta que, en tiempo t ≥ t0, el peso acumulativo de la transacción legítima es aproximadamente w0 +λw(t− t0) (recordemos que asumimos que el período de adaptación se ha terminado, por lo que el peso acumulativo sólo crece con la velocidad λw). Análogamente a (12) uno obtiene que la probabilidad de que la operación de doble gasto tenga más peso acumulativo a tiempo t ≥ t0 es aproximadamente.
Obsérvese que, típicamente, tenemos μ𝑡0/𝑤0 ≥ μ/𝑤𝜆 (ya que, durante el período de adaptación, el peso acumulado crece con una velocidad inferior a λw). De todos modos, se puede demostrar que la probabilidad de lograr un gasto doble exitoso es de orden
donde a ∨ b := max(a, b). Por ejemplo, m = w = 1, μ = 2, λ = 3 (para que la potencia del atacante sea sólo un poco menor que la del resto de la red). Suponga que la transacción obtuvo un peso acumulado de 32 por el tiempo 12. Entonces, μ𝑡0/𝑤0 ∨ μ/𝑤𝜆=(3/4) , ϕ (3/4) ≈ 0.03768, y (14) entonces da el límite superior aproximadamente 0.29. Si asumimos, sin embargo, que μ = 1 (y mantenemos intactos otros parámetros), entonces , μ𝑡0/𝑤0 ∨ μ/𝑤𝜆 = (3/)8 , ϕ (3/8) ≈ 0.3558, y (14) da aproximadamente 0.00001135, bastante cambio en verdad. De la discusión anterior es importante observar que, para que el sistema sea seguro, debería ser verdad que λw > μ (de lo contrario, la estimación (14) sería inútil); es decir, el flujo de entrada de transacciones "honestas" debería ser lo suficientemente grande en comparación con la potencia computacional del atacante. Esto indica la necesidad de medidas de seguridad adicionales (es decir, puestos de control) durante los primeros días de IOTA. Además, en cuanto a las estrategias para decidir cuál de las dos transacciones contradictorias es válida, hay que tener cuidado cuando se confía sólo en el peso acumulado. Esto se debe a que puede estar sujeto a un ataque similar al descrito en la Sección 4.1 (el atacante puede preparar una transacción de doble gasto con mucha anticipación, construir una subcadena/subTangle secreta haciendo referencia a ella, y luego transmitir esa subTangle después de que el comerciante acepte la transacción legítima). Más bien, un mejor método para decidir entre dos transacciones contradictorias podría ser el descrito en la siguiente sección: ejecute el algoritmo de selección de tips, y vea qué transacción de las dos es (indirectamente) aprobada por la tip seleccionada.
4.1 Ataque de una parasite chain y un nuevo algoritmo de selección de tips
Considere el siguiente ataque (Figura 6): un atacante construye secretamente una cadena/subTangle, ocasionalmente haciendo referencia a la Tangle principal para ganar más puntos (tenga en cuenta que la puntuación de las tips buenas es más o menos la suma de todos los pesos propios en la Tangle principal, mientras que la puntuación de las tips del atacante también contienen la suma de todos los pesos propios en la parasite chain).
Además, dado que la latencia de la red no es un problema para alguien con una computadora lo suficientemente potente que construye la cadena por sí sola11, el atacante podría ser capaz de dar más altura a las tips parásitas. Por último, el número de tips del atacante puede ser incrementado artificialmente en el momento del ataque (mediante la emisión de muchas transacciones que aprueban todas las transacciones del mismo atacante, véase la Figura 6 a continuación), en caso de que los nodos honestos usen alguna estrategia de selección que implique una simple elección entre las tips disponibles.
Para defenderse de este ataque, vamos a utilizar el hecho de que la Tangle principal se supone que tiene más poder de hashing (activo), y por lo tanto logra dar más peso acumulativo a más transacciones que el atacante. La idea es utilizar un algoritmo MCMC (Markov Chain Monte Carlo) para seleccionar las dos tips de referencia.
Sea Hx el peso acumulado actual de un sitio (es decir, una transacción representada en el gráfico de la Tangle). Recordemos que asumimos que todos los pesos propios son iguales a 1; por lo tanto, el peso acumulado de una tip es siempre 1, y el peso acumulado de otros sitios es al menos 2.
La idea es colocar algunas partículas (también conocidas como caminantes aleatorios) en sitios de la Tangle, y dejarlas caminar hacia las tips de una manera aleatoria12. Las tips "escogidas" por las caminatas son entonces las candidatas para la aprobación. El algoritmo se describe de la siguiente manera:
1. considere todas las transacciones con un peso acumulado entre W y (digamos) 2W (donde W es razonablemente grande, a elegir13);
2. Coloque las partículas N de forma independiente allí (N no es tan grande, digamos, 10 o así14);
3. Estas partículas realizarán caminatas aleatorias independientes y discretas "hacia las tips" (es decir, la transición de x a y es posible si y aprueba x);
4. Las dos caminatas aleatorias que lleguen primero a la tip fijada indicarán nuestros dos tips a aprobar;
Figura 6: En el algoritmo de selección de tips. Los dos círculos rojos indican un intento de doble gasto.
5. Las probabilidades de transición de los paseos se definen de la siguiente manera: si y aprueba x (nosotros denotamos este y --> x), entonces la probabilidad de transición Pxy es proporcional a exp − α(Hx − Hy), es decir
donde α > 0 es un parámetro a elegir (puede iniciarse p. ej. con α = 1).
En particular, tenga en cuenta que este algoritmo es "local", no es necesario ir hasta la génesis para calcular las cosas.
Para ver que el algoritmo funciona como se pretende, considere primero los "lazy tips" (aquellos que intencionalmente aprueban algunas transacciones viejas para evitar la verificación), vea la Figura 6. Obsérvese que, incluso si la partícula se encuentra en un sitio aprobado por tal tip, no es probable que la tip perezosa sea seleccionada, ya que la diferencia de pesos acumulativos será muy grande, mire (15).
A continuación, considere el siguiente ataque: el atacante construye secretamente una cadena (una "parasite chain") que contiene una transacción que vacía su cuenta a otra cuenta bajo su control (indicada como el círculo rojo más a la izquierda en la Figura 6). En algún momento el atacante emite una transacción en la Tangle principal (indicada como el otro círculo rojo), y espera hasta que el comerciante la acepta. La parasite chain a veces hace referencia a la Tangle principal (de ahí el nombre) y por lo tanto sus sitios tienen buenas altura/puntuación (incluso mejor que los de la Tangle principal), aunque el peso acumulativo no es tan grande en esa cadena. Tenga en cuenta también que no puede hacer referencia a la Tangle principal después de la transacción del comerciante. Además, el atacante podría tratar de inflar artificialmente el número de sus tips en el momento del ataque, como se muestra en la foto. La idea del atacante es hacer que los nodos hagan referencia a la parasite chain, para que la "buena" Tangle quede huérfana.
Ahora, es fácil ver por qué el algoritmo de selección MCMC con alta probabilidad no seleccionará una de las tips del atacante. Básicamente, la razón es la misma porque el algoritmo no selecciona las tips perezosas: los sitios de la parasite chain tendrán un peso acumulado mucho menor que los sitios de la Tangle principal a los que se refieren. Por lo tanto, no es probable que la caminata aleatoria vaya a saltar a la parasite chain (a menos que empiece allí, pero esto no es muy probable también, ya que la Tangle principal contiene más sitios).
A continuación, comentamos por qué los nodos seguirían (al menos aproximadamente) este algoritmo. Recordemos que, como se ha observado en la Sección 1, es razonable suponer que al menos una proporción "buena" de los nodos seguirá el algoritmo de referencia. Además, debido a retrasos computacionales y de red, el algoritmo de selección de tip preferiría trabajar con una snapshot pasada de la Tangle (con respecto al momento en que se emite la transacción). Ahora bien, puede ser una buena idea mover intencionalmente esta instantánea más al pasado15 en el algoritmo de referencia, por las razones que explicamos en la secuela. Imagine un nodo "egoísta" que sólo quiere maximizar las posibilidades de que su transacción sea aprobada en breve. El algoritmo MCMC de esta sección (adoptado por una proporción considerable de otros nodos) define una distribución de probabilidad en el conjunto de tips; claramente, una primera opción natural para ese nodo sería escoger las tips donde se alcanza el máximo de esa distribución. Sin embargo, si muchos otros nodos también se comportan de una manera egoísta (lo que es bastante razonable suponer también) y usan la misma estrategia, entonces todos ellos perderán: muchas transacciones nuevas aprobarán las mismas dos tips al mismo tiempo, por lo que habrá demasiada competencia entre ellos para su aprobación posterior (ya que los nodos usan una snapshot pasada, todavía no "sentirán" el aumento de peso acumulado causado por esta aprobación masiva de las dos tips). Por lo tanto, incluso un nodo egoísta tendría que usar algún algoritmo de aprobación aleatoria de la tip, y la distribución de probabilidad de las tips seleccionadas debería estar, en algún sentido,"no muy lejos" de la distribución de probabilidad por defecto (es decir, la producida por el algoritmo de selección de tip de referencia). No afirmamos que esta distribución de probabilidad "agregada" (en presencia de nodos egoístas) sería igual a la distribución de probabilidad por defecto, pero el argumento anterior muestra que debería estar cerca de ella. Esto significa que la probabilidad de seleccionar "malas" tips permanecería pequeña. En cualquier caso (diferente a Bitcoin), no hay tanto incentivo para que los nodos sean egoístas, ya que las posibles ganancias sólo suponen una ligera disminución en el tiempo de confirmación. Además, no se establece en stone que las probabilidades de transición deban definirse necesariamente como en (15). En lugar del exponente, se puede tomar otra función que disminuye rápidamente, como p. ej. f (s) = s -3. Hay mucha libertad para la elección de W y N también. De hecho, la sensación del autor es que la contribución principal de esta sección es la idea misma de usar MCMC para la selección de tips; no está claro si hay algún argumento "teórico" que muestre exactamente de qué manera deben elegirse estos parámetros.
4.2 Splitting attack
El siguiente esquema de ataque contra el algoritmo MCMC arriba mencionado fue sugerido por Aviv Zohar. En el régimen de alta carga, un atacante puede intentar dividir la Tangle en dos ramas y mantener el equilibrio entre ellas, para que ambas sigan creciendo. Para evitar que un nodo honesto haga referencia a las dos ramas a la vez (agrupándolas efectivamente), el atacante debe colocar al menos dos transacciones conflictivas al principio de la división. Entonces, espera que aproximadamente la mitad de la red contribuya a cada rama, para poder "compensar" las fluctuaciones aleatorias incluso con una potencia de computación relativamente pequeña. Entonces, el atacante podría gastar los mismos fondos en las dos ramas. Para defenderse contra tal ataque, uno necesita usar alguna regla de "umbral agudo" (como "seleccionar la cadena más larga" en Bitcoin) que hace demasiado difícil mantener el equilibrio entre las dos ramas. Sólo para dar un ejemplo, supongamos que una rama tiene el peso total (o cualquier otra métrica que podamos usar) 537, y el peso total de la otra rama está bastante cerca, digamos, 528. Si en tal situación un nodo honesto selecciona la primera rama con probabilidad muy cercana a 1/2, entonces, probablemente, el atacante sería capaz de mantener el equilibrio entre las ramas. Sin embargo, si un nodo honesto prefiere la primera rama con una probabilidad considerablemente mayor que 1/2, entonces el atacante probablemente no podría mantener el equilibrio, porque después de una fluctuación aleatoria inevitable la red rápidamente escogerá una de las ramas y abandonará la otra. Claramente, para que el algoritmo MCMC se comporte de esta manera, uno tiene que elegir una función de decaimiento muy rápido f, y también iniciar el paseo aleatorio en un nodo con una profundidad (relativamente) grande (de modo que es probable que empiece antes de que se haya creado la división). En este caso, la caminata aleatoria elegiría la rama "más pesada" con gran probabilidad, aunque la diferencia de peso total entre las ramas sea pequeña. Cabe señalar que la tarea del atacante es muy difícil también debido a los problemas de sincronización de la red: es posible que no esté al tanto de una buena parte de las transacciones recientemente emitidas16. Otra forma efectiva de evitar semejante ataque sería que una entidad lo suficientemente poderosa publique un gran número de transacciones a la vez (en una rama), cambiando rápidamente el equilibrio de poder y haciendo difícil que el atacante se enfrente a este cambio. Obsérvese también que, si el atacante logra mantener la división, las transacciones recientes sólo tendrán alrededor del 50% de la confianza de confirmación (recordar la Sección 1), y no crecerá; por lo tanto, los nodos "honestos" pueden decidir entonces comenzar a aprobar sólo las transacciones pre-split (y, en particular, no aprobar ninguna de las dos transacciones en conflicto). Se pueden considerar otras modificaciones del algoritmo de selección de tips. Por ejemplo, si un nodo ve dos subTangles grandes, primero elige la que tiene mayor suma de pesos propios, y luego hace la selección de la tip sólo allí usando el algoritmo MCMC anterior. Además, la siguiente idea puede ser digna de consideración: hacer que las probabilidades de transición en (15) dependan no sólo de Hx - Hy, sino también de Hx, de tal manera que el siguiente paso de la cadena Markov sea casi determinístico cuando el caminante está en lo profundo de la Tangle (para evitar entrar en la rama más débil), sino que se difunda más cuando está cerca de las tips (para que haya suficiente aleatoriedad en la elección de las dos transacciones a aprobar).
Conclusiones:
1. Consideramos algunas estrategias de ataque, cuando el atacante intenta el doble gasto haciendo "outpacing" del sistema.
2. El "large weight attack" significa que, para poder gastar el doble, el atacante intenta dar un peso muy grande a la transacción de doble gasto, por lo que solo superaría la subtangle legítima. Esta estrategia sería una amenaza para la red en caso de que el peso propio permitido no tenga límites. Como solución, podemos limitar el propio peso de una transacción desde arriba, o incluso ponerla en constante.
3. En la situación en la que el máximo peso propio de una transacción es m, la mejor estrategia del atacante es generar siempre transacciones con el máximo peso propio que haga referencia a la transacción de doble gasto. Cuando el flujo de entrada de transacciones "honestas" es lo suficientemente grande en comparación con la potencia computacional del atacante, la probabilidad de que la transacción de doble gasto tenga un mayor peso acumulativo puede estimarse utilizando la fórmula (14) (véanse también los ejemplos siguientes (14)).
4. El ataque basado en la construcción de una "parasite chain" hace obsoletas las estrategias de aprobación basadas en la altura o la puntuación, ya que el atacante obtendrá valores superiores a los de la Tangle legítima. Por otro lado, el algoritmo de selección de tip MCMC descrito en la Sección 4.1 parece proteger bien contra este tipo de ataque.
5. Como bonus, también ofrece protección contra los "nodos perezosos", es decir, aquellos que sólo aprueban algunas transacciones antiguas para evitar hacer los cálculos necesarios para validar la Tangle.4.3 Resistencia a los cálculos cuánticos
Se sabe que un ordenador cuántico (hoy todavía hipotético) suficientemente grande puede ser muy eficaz para manejar problemas donde la única manera de resolverlos es adivinar las respuestas repetidamente y comprobarlas. El proceso de encontrar un nonce para generar un bloque de Bitcoin es un buen ejemplo de tal problema. A día de hoy, en promedio se deben comprobar alrededor de 268 nonces para encontrar un hash adecuado que permita generar un bloque. Se sabe (véase por ejemplo[13]) que un ordenador cuántico necesitaría Θ(√ N) operaciones para resolver un problema del tipo anterior que necesita (N) operaciones en un ordenador clásico. Por lo tanto, una computadora cuántica sería alrededor de √268 = 234 ≈ 17 mil millones de veces más eficiente en la minería de Bitcoin que una clásica. Además, vale la pena señalar que si la blockchain no aumenta su dificultad en respuesta al aumento del poder de hashing, eso llevaría a una mayor tasa de bloques huérfanos. Observe que, por la misma razón, el "large weight attack" descrito anteriormente también sería mucho más eficiente en un ordenador cuántico. Sin embargo, limitar el peso desde arriba (como se sugiere en la Sección 4) también podría limitar un ataque de computadora cuántica, debido a la siguiente razón. En IOTA, el número de nonces que uno necesita comprobar para encontrar un hash adecuado para emitir una transacción no es tan grande, sólo está alrededor de 38. La ganancia de eficiencia para una computadora cuántica "ideal" sería por lo tanto de orden 34 = 81, que ya es bastante aceptable (también, recuerde que Θ(√ N) podría significar fácilmente 10√ N o así). Además, el algoritmo es tal que el tiempo para encontrar un nonce no es mucho mayor que el tiempo necesario para otras tareas necesarias para emitir una transacción, y la última parte es mucho más resistente contra la computación cuántica. Por lo tanto, la discusión anterior sugiere que la Tangle proporciona una protección mucho mejor contra un adversario con una computadora cuántica en comparación con la Blockchain (Bitcoin).
Notas:
1 este es el enfoque más simple; uno también puede estudiar sistemas similares donde las transacciones deben aprobar k ≥ 2, o considerar reglas más complicadas
2 si un nodo emite una nueva transacción que aprueba transacciones conflictivas, entonces corre el riesgo de que otros no aprueben esta nueva transacción, por lo que caerá en el olvido.
3 comentamos más sobre esto al final de la Sección 4.1
4 es decir, transacciones emitidas de acuerdo con el protocolo
5 como se mencionó anteriormente, hay una buena razón para asumir que otros nodos seguirían (casi) el mismo algoritmo para la selección de la tip
6 este intervalo también debe ser finito - ver "ataque de gran peso" en la Sección 4
7 bajo una suposición adicional de que el proceso es homogéneo en el tiempo
8 recordamos al lector que no intentamos imponer ninguna estrategia de selección de tips en particular, así que un el atacante puede elegir tips de cualquier manera que le resulte conveniente
9 De hecho, el sentimiento del autor es que la estrategia de aprobación de tips es el ingrediente más importante para construir una cripto tangle-based. Es allí donde se esconden muchos vectores de ataque. Además, dado que generalmente no hay manera de hacer cumplir una estrategia de aprobación de tips en particular, debe ser tal que los nodos voluntariamente elijan seguirla sabiendo que al menos una buena proporción de otros nodos lo hacen.
10 o incluso antes; discutiremos este caso más tarde.
11 esto se debe a que el atacante siempre puede aprobar sus propias transacciones, sin depender de ninguna información del resto de la red.
12 no hay ninguna fuente "canónica" de aleatoriedad; los nodos sólo usan sus propios generadores de números (pseudo)aleatorios para simular las caminatas aleatorias
13 La idea es colocar la partícula "profundo" en la Tangle (de manera que no llegue a una tip de inmediato) pero no "demasiado profundo" (de manera que encuentre una tip en un tiempo razonable). Además, el intervalo [W, 2W] es arbitrario, se puede elegir p. ej.[W, 3W] en su lugar, o lo que sea.
14 Una vez más, esta elección es en gran medida arbitraria; utilizamos varias partículas en lugar de sólo dos para mayor seguridad. La idea es que una partícula salta accidentalmente a la cadena del atacante (que se supone que es larga), entonces pasará mucho tiempo allí y se elegirán primero otros tips.
15 es decir, primero la caminata aleatoria encuentra una tip (pasada) con respecto a esa snapshot, y luego continúa caminando hacia las tips "reales" en la Tangle actual.
16 así que los pesos acumulativos "reales" pueden ser muy diferentes de lo que él/ella cree
[1] Iota: a cryptocurrency for Internet-of-Things. See http://www.iotatoken.com/, and
https://bitcointalk.org/index.php?topic=1216479.0
[2] bitcoinj. Working with micropayment channels. https://bitcoinj.github.io/working-withmicropayments
[3] people on nxtforum.org (2014) DAG, a generalized blockchain. https://nxtforum.org/proof-ofstake-algorithm/dag-a-generalized-blockchain/
(registration at nxtforum.org required)
[4] Moshe Babaioff, Shahar Dobzinski, Sigal Oren, Aviv Zohar (2012) On Bitcoin and red balloons.
Proc. 13th ACM Conf. Electronic Commerce, 56–73.
[5] Sergio Demian Lerner (2015) DagCoin: a cryptocurrency without blocks.
https://bitslog.wordpress.com/2015/09/11/dagcoin/
[6] Yonatan Sompolinsky, Aviv Zohar (2013) Accelerating Bitcoin’s Transaction Processing. Fast
Money Grows on Trees, Not Chains. https://eprint.iacr.org/2013/881.pdf
[7] Yoad Lewenberg, Yonatan Sompolinsky, Aviv Zohar (2015) Inclusive Block Chain Protocols.
http://www.cs.huji.ac.il/~avivz/pubs/15/inclusive btc.pdf
[8] Joseph Poon, Thaddeus Dryja (2016) The Bitcoin Lightning Network: Scalable Off-Chain Instant
Payments. https://lightning.network/lightning-network-paper.pdf
[9] Sheldon M. Ross (2012) Introduction to Probability Models. 10th ed.
[10] David Vorick (2015) Getting rid of blocks. slides.com/davidvorick/braids
[11] Amir Dembo, Ofer Zeitouni (2010) Large Deviations Techniques and Applications. Springer.
[12] Sheldon M. Ross (2009) A First Course in Probability. 8th ed.
[13] Gilles Brassard, Peter Hyer, Alain Tapp (1998) Quantum cryptanalysis of hash and claw-free
functions. Lecture Notes in Computer Science 1380, 163– 169.
Fuente: Artículo traducido al español por Gerónimo Patat en: http://www.iotahispano.com/wp-content/uploads/2017/11/IOTA_Whitepaper_ESP.pdf
La presente es una transcripción de su original. PandectasDigital no se hace responsable por cualquier discrepancia u omisión contenida en ella, ni por los daños o perjuicios que pudieran causarse por su uso, ni por su reproducción total o parcial.
A continuación, su versión actualizada (October 1, 2017. Version 1.3) en idioma original publicada en https://iota.org:
Oprime AQUÍ para descargar el documento
Oprime AQUÍ para descargar el documento
Oprime AQUÍ para descargar el documento















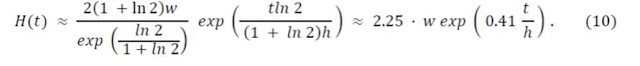














![Ley de Regulación del Arrendamiento Inmobiliario para el uso Comercial <span face=""b612" , sans-serif"><span style="color: black; font-weight: normal;"><i>[</i></span><span style="color: #04ff00;"><b><i>Vigente</i></b></span><span style="color: black; font-weight: normal;"><i>]</i></span></span>](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjsBK4q93bBA7A-xxLjoSiwG9CGWwiG8VtwzlRvdKLaIK1Qq28WD2BkyZVNKe241zLniUqAS9eByWuFtXthM6JWc96RSocXgeYLJjKKPW__ZuR1EzE776N3BJeGKmm7smSiIJevSxwf1sU/w100/Escudo+Nacional_opt4x4.jpg)
![Ley de Disciplina Militar <span face=""b612" , sans-serif"><span style="color: black; font-weight: normal;"><i>[</i></span><span style="color: #04ff00;"><b><i>Vigente</i></b></span><span style="color: black; font-weight: normal;"><i>]</i></span></span>](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjBw7D-mnNiCiUaYhi-g_5bXn5-O_ybbTwHtIt5qGiwuCn4hQcflkUbUKNMcLWOrn8lJvTeFcqnxhAIlkvWTgVj6F2PQscUT5f6wP-GIVxroc4do1NZzLlJJdKCxcePhVcbvr-tPN4mLbc/w100/AN_opt4x4.jpg)